The signals coming from the Hall effect sensors need to be scaled and are non-linear. In order to make them behave the same way potentiometers we need to linearize them. We do this with a 3rd order polynomial fit.

Imagine we move the stick into the 8 different gate notches and record the x-position at each location. We would expect to get the values -1.0,-0.71,0,0.71, and 1.0, depending on which notch we were in. But with the hall effect sensors we might get something else, we might get -0.63,-0.52,0.0,0.29, and 0.33 for example.

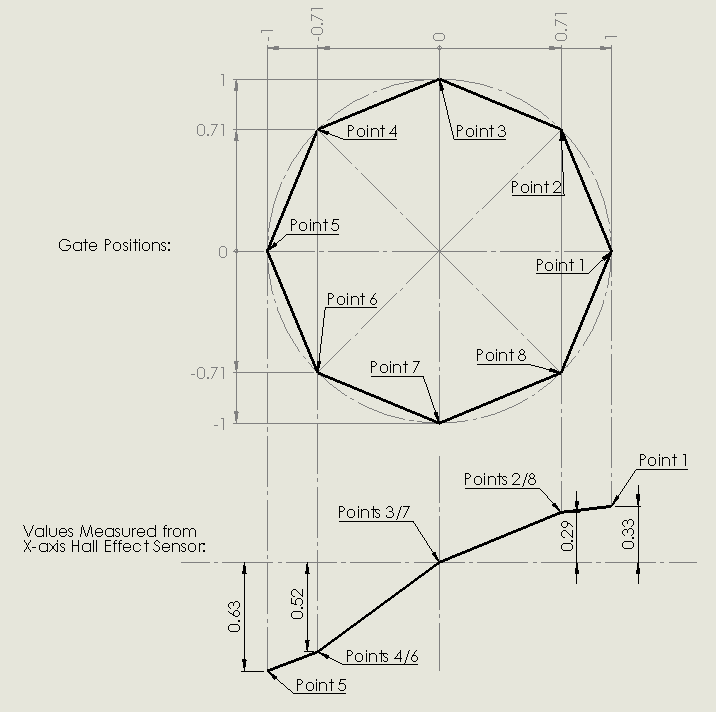
But since we know what the values should be, we can find an equation which transforms the values from the hall sensor into the values we want:

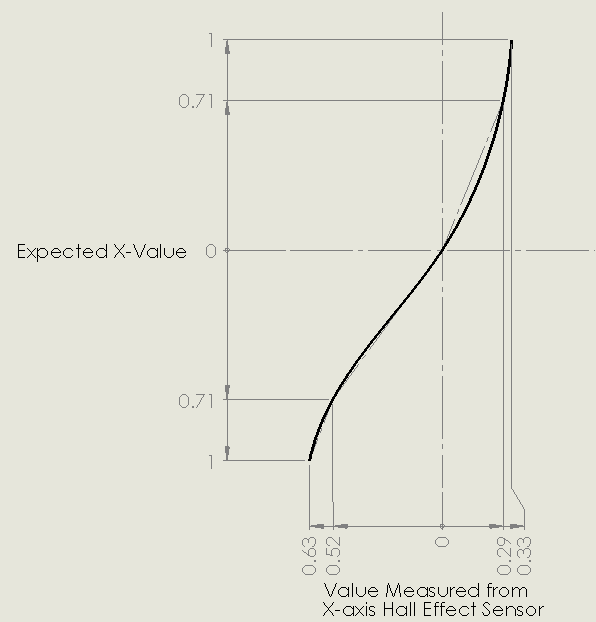
The simplest function that appears to do a reasonable job of fitting the hall effect sensor data has been a 3rd order polynomial of the form Ax^3 + Bx^2 + Cx + D. Using these x-values measured at the gate notches we can find the coefficients A,B,C,D through regression analysis (usually ordinary least squares), then we just substitute the value we got from the sensor into x, and we get the linearized output.

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.